Developed in collaboration with Andrew Curtis; Schlumberger Cambridge Research, Cambridge CB3 0EL, England; curtis@cambridge.scr.slb.com
The oct-tree importance sampling algorithm gives accurate, efficient and complete mapping of earthquake location PDFs in 3D space (x-y-z).
Advantages:
Drawbacks:
The oct-tree method uses recursive subdivision and sampling of cells in 3D space (below) to generate a cascade of sampled cells, where the density of sampled cells follows the PDFvalues of the cell centre.

The probability that the earthquake location is in a given cell i is approximately,
Pi= Vi PDF(xi)
where Vi is the cell volume and xi is the coordinates of the cell centre.
The core of the method is an ordered list LP of probability values Pi for all previously sampled cells:

The oct-tree sampling procedure is initialised by a global sampling of the full search space on a coarse, regular grid (B below). The misfit value gi(x) at the centre of each grid cell is determined, the probability Pi is calculated, and the cell is inserted in the probability list LP at the position corresponding to its probability Pi .
Next the following steps are repeated (C-E below) until a predetermined number of evaluations of the forward problem or other termination criterion has been reached:
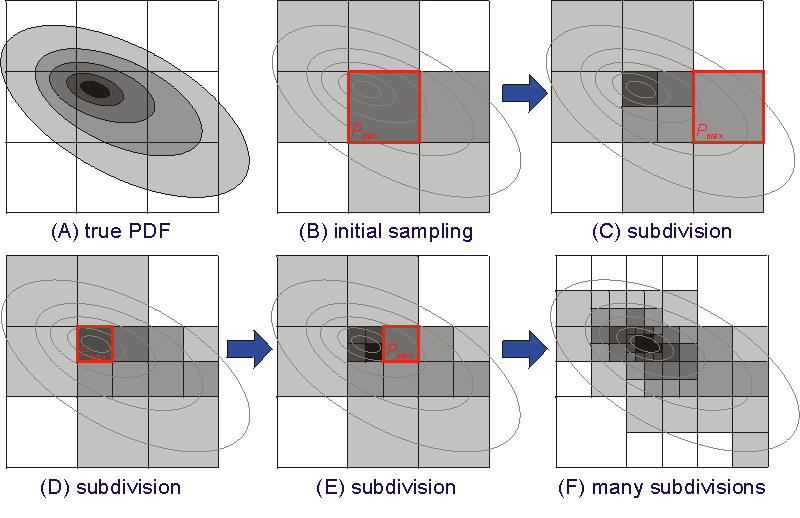
This recursive procedure converges rapidly, producing an oct-tree structure of cells specifying location PDF values in 3D space (F above). This oct-tree structure will have a larger number of cells in the regions of higher PDF (lower misfit) and thus gives approximate importance sampling of the PDF (A above).
Finally, samples in 3D drawn from the oct-tree structure (below) give a useful and compact representation of the PDF.

The example below is illustrated by 2D projections of such 3D samples.
An exhaustive grid-search (below, left) shows the complete PDF for the location; this PDF shows two distinct regions of high probability at different depths. The oct-tree method (right) identifies both solution volumes and is thus more complete than a Metropolis-simulated annealing approach (centre), which identifies only the deeper solution. Both of these methods are about 100 times faster than the grid search, but only the oct-tree method produces an image of the solution PDF that is nearly identical to that of the exhaustive grid-search. The oct-tree and Metropolis-simulated annealing methods are only about 10 times slower than standard linearised location algorithms, which are difficult or impossible to apply with 3D models.

An image of all cell centres visited by the oct-tree method (blow, left) shows that this method samples globally while producing efficient importance sampling: i.e. The distribution of cell centres follows closely the distribution of samples of the final PDF (right).

The oct-tree method performs well for the earthquake location problem because it is 3D. This allows the use of the simple geometry of oct-tree division of rectangular cells: the volume of each cell is always known and it can be determined easily which cell contains a given point. The oct-tree method should be applicable in 4D, allowing a search over origin time. But in higher dimensional problems the determination of the volume of a cell and whether or not a cell contains a given point may become difficult or impossible.
The oct-tree approach can be applied to teleseismic location in a spherical earth by a) performing the location in a cubic region containing the spherical earth, or b) dividing the spherical earth into organized curvilinear cells which can be further sub-divided into 8 child cells.